आज हम computer in hindi मे आज हम boolean algebra in hindi - computer system architecture in hindi के बारे में जानकारी देगे क्या होती है तो चलिए शुरु करते हैं- के बारे में जानकारी देगे क्या होती है तो चलिए शुरु करते हैं-
boolean algebra in hindi:-
boolean algebra एक algebra (set, operations , elements) है जिसमें 22 element के साथ एक set B होता है, जिसमें तीन operations होते हैं- और operation (Boolean product), या operation + (Boolean sum), और Operation नहीं '( पूरक) - set पर परिभाषित, जैसे कि किसी भी element के लिए A,B,C और A 'B में हैं। चार-elemet boolean algebra B पर करें, = ({0, x, y, 1}; , +, '; 0, 1)। AND, OR, और NOT Operation को explain किया गया है।
दो-element boolean algebra B पर करें, = ((0, 1};., +, '; 0, 1)। तीन operations:-(AND), + (OR), '(NOT) को किया गया है:-
boolean function in hindi:-
दो- element boolean algebra B, अन्य सभी B के बीच, जहां i> 2, स्विचिंग algebra के रूप में define सबसे उपयोगी है। स्विचिंग algebra में दो तत्व होते हैं जिन्हें क्रमशः 1 और 0 द्वारा सबसे बड़ी संख्या और सबसे छोटी संख्या के रूप में define किया जाता है।
boolean algebra एक स्विचिंग algebra है जो binary variable और logic operation से releted है। variables को A,B,X और Y जैसे अक्षरों द्वारा नामित किया गया है। तीन basic logic operation हैं AND, OR, और पूरक। एक boolean function को बाइनरी वेरिएबल्स, लॉजिक ऑपरेशन सिंबल, brackets और equal sign के साथ बीजगणितीय रूप से व्यक्त किया जा सकता है। variable के दिए गए मान के लिए, boolean function या तो 1 या 0 हो सकता है।
Example of boolean function in hindi:-
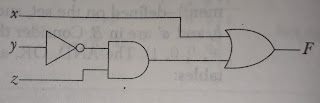
F = x+y'z
function F 1 के बराबर है यदि x 1 है या यदि y और z दोनों 1 के बराबर हैं; या बराबर 0 अन्यथा। लेकिन यह कहना कि y' y का Supplement है। इसलिए, हम कह सकते हैं कि 1 के बराबर है यदि x = 1 या यदि yz = 01 है। एक फ़ंक्शन और उसके binary variable के बीच संबंध को एक trust table मे define किया जा सकता है। एक trust table में एक फ़ंक्शन का Representation करने के लिए हमें एन binary variable के 2 "combinations की एक list की आवश्यकता होती है। बिट्स को icon करने के लिए आठ संभावित अलग-अलग combinations हैं। तीन function x, y, और z। उन combinations के लिए 1 के बराबर function जहां x = 1 या yz = 01; यह अन्य सभी combinations के लिए 0 के बराबर है। 1 यह कहने के बराबर है कि y = 0 क्योंकि y है ।
Truth table of boolean function in hindi:-
Logic diagram:-
एक Boolean function को Algebraic Expression से AND, OR, और inverter gates से बना एक Logic diagram में परिवर्तित किया जा सकता है। F के लिए Logic diagram दिखाया गया है। इसे उत्पन्न करने के लिए इनपुट y के लिए एक इन्वर्टर है Supplement Y'। Y'z शब्द के लिए एक AND गेट है, और दो शब्दों को मिलाने के लिए एक OR गेट का उपयोग किया जाता है। एक Logic diagram में, फ़ंक्शन के Variable को Circuit के इनपुट के रूप में लिया जाता है, और फ़ंक्शन के Variable symbol को सर्किट के आउटपुट के रूप में लिया जाता है।
Boolean function का उद्देश्य डिजिटल सर्किट के विश्लेषण और डिजाइन को सुविधाजनक बनाना है। एक truth table द्वारा Specified एक Boolean function को algebraic रूप से अलग-अलग रूप में define किया जा सकता है boolean expression बनाने के दो तरीके विहित और कई गैर-विहित रूप हैं। विहित रूप Boolean function के प्रत्येक product (AND) या योग (OR) पद में सभी बाइनरी Variable को define करते हैं। एक Boolean function F(A, B, C) = A'B +C + ABC, जो non-canonical रूप में है, product के विहित योग का निर्धारण करने के लिए, उपयोग किया जाता है।
F = A'B + C' + ABC
= A'B(C + C') + (A + A')(B + B')C' + ABC,
where x + x' = 1 is a basic identity of Boolean algebra in hindi:-
= A'BC+ A'BC' + ABC' + AB'C' + A'BC' + A'B'C' + ABC
= A'BC + A'BC + ABC' + AB'C' + A'B'C' + ABC
Boolean algebra नियमों के अनुसार boolean expression में हेर-फेर करके, कोई एक Simple expression प्राप्त कर सकता है जिसके लिए कम Gates की आवश्यकता होगी। यह देखने के लिए कि यह कैसे किया जाता है, हमें पहले boolean algebra की जोड़-तोड़ क्षमताओं का Study करना चाहिए। boolean algebra की सबसे बुनियादी पहचान Listed करती है। table में सभी पहचान true table के माध्यम से सिद्ध की जा सकती हैं। पहली आठ सर्वसमिकाएँ Single variable और स्वयं के बीच Original relationship को define करती है।
Basic Identities of Boolean Algebra in hindi:-
(1) x + 0 = x
(2) x·0 = 0
(3) x + 1 = 1
(4) x·1 = x
(5) x + x = x'
(6) x• x = x
(7) x + x' = 1
(8) x·x' = 0
(9) x + y = y + x
(10) xy = yx
(11) x + (y+ z) = (x+y) + z
(12) x(yz) = (xy) z
(13) x (y + z) = xy + xz
(14) x + yx (x + y)(x + z)
(15) (x + y)' = x'y'
(16) (x) = x' + y'
(17) (x')' = x



टिप्पणियाँ
एक टिप्पणी भेजें