आज हम computer in hindi मे आज हम de morgan's theorem in hindi - computer system architecture in hindi के बारे में जानकारी देगे क्या होती है तो चलिए शुरु करते हैं-
de morgan's theorem in hindi:-
de morgan's theorem, NOR और NAND gates से tackle में बहुत महत्वपूर्ण है। इसमें कहा गया है कि एक NOR गेट जो (x + y)' function करता है, function x'y के बराबर होता है। इसी प्रकार, एक NAND function को या तो (xy)' या (x + y') द्वारा define किया जा सकता है। इस कारण से NOR और NAND गेट के दो अलग-अलग graphic symbol हैं, एक Circle के बाद एक या graphic symbol के साथ एक AND OR gates का Representation करने के बजाय, हम सभी इनपुट में Circle से पहले और graphic symbol द्वारा इसका Representation कर सकते हैं। AND OR gates के लिए उलटा-और प्रतीक de morgan's theorem से और इस seminar से है कि छोटे Circle complementarity को define हैं। इसी तरह, NAND gate के दो अलग-अलग प्रतीक हैं। NAND और NOR गेट का उपयोग किसी भी boolean function को लागू करने के लिए किया जा सकता है, जिसमें AND, OR, और NOT जैसे basic logic gate शामिल हैं। इसलिए, NAND और NOR गेट को यूनिवर्सल गेट कहा जाता है।
यह देखने के लिए कि डिजिटल सर्किट को सरल बनाने के लिए boolean algebra हेरफेर का उपयोग कैसे किया जाता है। सर्किट के आउटपुट को algebraic रूप से define किया जा सकता है-
F = ABC+ABC'+A'C
प्रत्येक शब्द एक और gates से मेल खाता है, और OR gates तीन शब्दों का logical sum बनाता है। A के Supplement के लिए दो इनवर्टर की आवश्यकता होती है ' और C'। boolean algebra का उपयोग करके Expression को सरल बनाया जा सकता है।
F=ABC+ABC'+A'C = AB(C+C') + A'C = AB + A'C
परिपथ में प्रयुक्त six gates के बजाय केवल four gates की आवश्यकता है। दो सर्किट Equivalent हैं और इनपुट A,B,C और आउटपुट F के बीच एक ही truth table relationship generated करते हैं।
Complement of a function:-
एक function का Supplement एक truth table में define किए जाने पर function F का Supplement मूल्यों में L और O को इंटरचेंज करके प्राप्त किया जाता है truth table को फिन करें। जब फ़ंक्शन को बीजीय रूप में define किया जाता है, तो फ़ंक्शन का Supplement demorgan theorem के माध्यम से प्राप्त किया जा सकता है। demorgan theorem का सामान्य रूप इस प्रकार define किया जा सकता है।
(X1+X2+X3+....+Xn)' = X1'X2'X3'....Xn'
(X1X2X3...Xn)' = X1'+X2'+X3'+.......+Xn'
सामान्य demorgan theorem से हम एक algebraic expression के Supplement को प्राप्त करने के लिए एक सरल प्रक्रिया प्राप्त कर सकते हैं। यह सभी OR ऑपरेशंस को AND ऑपरेशंस में और सभी AND ऑपरेशंस को OR ऑपरेशंस में बदलकर और फिर प्रत्येक व्यक्तिगत वेरिएबल को Supplement करके किया जाता है।
Example:-
F = AB + C'D' + B'D
F' = (A' + B')(C + D)(B + D')
Supplement व्यंजक AND और OR operations को आपस में बदलकर और प्रत्येक व्यक्तिगत variable को Supplement करके प्राप्त किया जाता है। ध्यान दें कि C', C का पूरक।
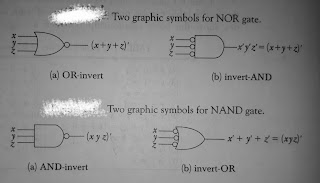

टिप्पणियाँ
एक टिप्पणी भेजें